Nauczyciele matematyki stoją przed trudnym wyzwaniem, gdyż uczniowie bardzo często mylą ze sobą pojęcia takie jak: średnia, mediana i dominanta (modalna, moda). Chociaż wszystkie są miarami tendencji centralnej, istnieją istotne różnice w tym, co każdy z nich oznacza i jak są obliczane. Zapoznaj się z kilkoma przydatnymi wskazówkami, które pomogą Ci rozróżnić te zagadnienia. Zapraszamy do artykułu pt. “Czym jest i jak obliczyć medianę, średnią i dominantę?”
Przejdź na skróty:
Definicja średniej, mediany i dominanty
Zrozumienie różnic między średnią, medianą i dominantą należy zacząć od zdefiniowania terminów, którymi będziemy się posługiwać, w sposób zrozumiały i łatwo przyswajalny. Dlatego:
- Średnia jest średnią arytmetyczną zbioru podanych liczb.
- Mediana to średni wynik w zestawie podanych liczb.
- Dominanta to najczęściej występujący wynik w zestawie podanych liczb.
Jak obliczyć średnią arytmetyczną?
Średnia lub średnia arytmetyczna jest obliczana poprzez zsumowanie wszystkich wyników i podzielenie sumy przez ich liczbę.
Przykład: W zestawie następujących liczb: 10 11 13 15 16 23 26, średnia arytmetyczna jest obliczana w następujący sposób:
(10+11+13+15+16+23+26) / 7 = 114 / 7 = 16,28
Średnia arytmetyczna zbioru liczb wynosi 16,28.
Jak obliczyć medianę?
Mediana to średni wynik rozkładu. Aby obliczyć medianę należy:
- Ułożyć liczby w kolejności numerycznej,
- Policzyć ilość liczb,
- w przypadku liczby nieparzystej, podziel przez 2 i zaokrąglij w górę, aby uzyskać pozycję mediany.
- w przypadku liczby parzystej, należy podzielić przez 2. Następnie przejdź do liczb na tej pozycji i uśrednij ją z liczbą na wyższej pozycji, aby uzyskać medianę.
Pamiętaj, że medianą jest po prostu środkowa liczba danego zbioru.
Przykład: Jaka jest mediana następującego zestawu liczb: 5, 7, 9, 9, 11?
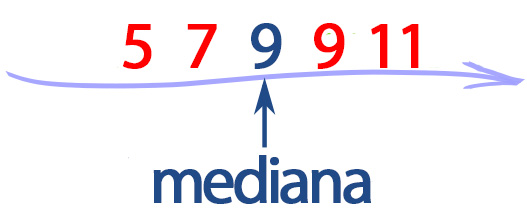
ilość liczb / 2 = 5 / 2 = 2,5 ≈ 3
Medianą jest liczba na trzeciej pozycji w tym zbiorze, 9.
Co w takim razie się dzieje, gdy masz parzystą liczbę wyników, więc nie ma jednego średniego wyniku? Należy zatem rozważyć kolejny przypadek.
Przykład: Jaka jest mediana następującego zestawu liczb: 1, 2, 2, 4, 5, 7?
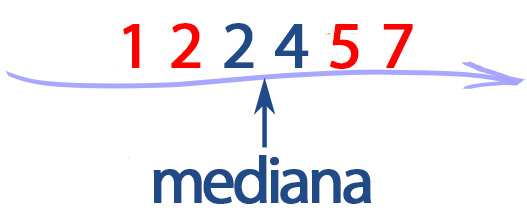
ilość liczb / 2 = 6 / 2 = 3
(2+4) / 2 = 3
Medianą jest średnia liczb 2 i 4, czyli 3.
Jak obliczyć dominantę?
Dominanta (modalna, moda) to najczęściej występująca partytura w rozkładzie. Wystarczy więc znaleźć najczęściej powtarzającą się liczbę jako dominantę.
Przykład: Znajdź dominantę następującego rozkładu liczb 2, 3, 6, 3, 7, 5, 1, 2, 3, 9.
Ponieważ liczba 3 występuje aż 3 razy, w porównaniu do drugiej najczęściej występującej liczby 2 w tym zbiorze, to właśnie ona jest dominantą. Pamiętaj jednak, iż w przypadku bardziej zaawansowanych zbiorów można stworzyć rozkład częstotliwości liczb, czyli określić ile razy dana liczba wystąpiła.
1-1x , 2-2x, 3-3x, 5-1x, 7-1x, 7-1x, 9-1x
W niektórych zestawach liczb w rzeczywistości mogą istnieć dwie dominanty. Taki rozkład będzie miał charakter bimodalny i występuje, gdy istnieją dwie liczby, których częstotliwość jest taka sama.
Przykład: Znajdź dominantę następującego zestawu liczb: 13, 17, 20, 20, 21, 23, 23, 26, 29, 30.
W tym zestawie zarówno liczba 20, jak i liczba 23 występują dwa razy. Są to dominanty tego zbioru liczb.
Uwaga! Jeśli żadna liczba w zestawie nie występuje więcej niż raz, to może nie być dominanty dla tego zestawu danych w ogóle!
Jak ocenić, której miary użyć?
Jeśli już wiemy jak obliczyć medianę, średnią i dominantę (modalną), a na dodatek wiemy co oznaczają, jak ocenić sposobność ich użycia? Otóż, każda z tych miar ma swoje słabe i mocne strony:
- Średnia wykorzystuje wszystkie liczby w zbiorze do wyrażenia miary tendencji centralnej, lecz wartości odstające mogą zniekształcić ogólną miarę, np.: kilka wyjątkowo wysokich wyników może przekrzywić średnią, tak że średni wynik wydaje się znacznie wyższy niż większość wyników w rzeczywistości jak np. średnie wynagrodzenia prezesów firm.
- Mediana pozbywa się nieproporcjonalnie wysokich lub niskich wyników, ale może nie mówić nic o pozostałej części zbioru.
- Dominanta może w mniejszym stopniu podlegać wpływom wartości odstających i jest idealna do reprezentacji tego, co jest „typowe” dla danej grupy liczb. Jednakże może być mniej przydatna w przypadkach, gdy żadna liczba nie występuje więcej niż raz lub liczba powtórzeń dominanty jest nieznacznie większa niż pozostałych liczb.
Wyobraź sobie sytuację, w której agent nieruchomości musi scharakteryzować swoje ogłoszenia na podstawie tendencji miar centralnej. W zbiorze znajdują się zatem następujące kwoty:
- 120 000 zł
- 120 000 zł
- 150 000 zł
- 270 000 zł
- 330 000 zł
- 380 000 zł
- 750 000 zł
- 755 000 zł
Średnia dla tej grupy wynosi 359 375 zł, mediana to 300 000 zł, a tryb 120 000 zł. Co Twoim zdaniem będzie najlepszą miarą? Jeśli chcesz uzyskać najwyższą liczbę, średnia jest zdecydowanie najlepszą opcją, nawet jeśli suma jest zniekształcona przez dwie bardzo wysokie liczby. Dominanta w tym przypadku nie byłby jednak dobrym wyborem, ponieważ jest nieproporcjonalnie niska w stosunku do pozostałych liczb. Zaś mediana wydaje się dość dobrym wskaźnikiem „typowych” cen sprzedaży wszystkich ofert nieruchomości. Wszystko zatem w dużej mierze zależeć będzie od sytuacji co i w jaki sposób chcemy przedstawić.
Masz jakieś pytania do artykułu pt. “Czym jest i jak obliczyć medianę, średnią i dominantę?” lub jakieś zagadnienie nie zostało do końca wyjaśnione? Napisz w komentarzu, a odpowiemy możliwie najszybciej!







