Pole figury geometrycznej jest zdefiniowane jako miara przestrzeni zamkniętej lub objętej danym kształtem w płaszczyźnie dwuwymiarowej. Romb to specjalny rodzaj równoległoboku, którego wszystkie boki są sobie równe. Romb można odróżnić od kwadratu miarą jego kąta wewnętrznego. Pole powierzchni rombu można obliczyć na różne sposoby, w zależności od znanych nam parametrów. Dowiedz się jaki jest wzór na pole rombu, jak obliczyć jego obwód i długość przekątnych!
Przejdź na skróty:
Co to jest pole rombu i jakie ma właściwości?
Pole rombu można zdefiniować jako ilość przestrzeni zamkniętej rombem w przestrzeni dwuwymiarowej. Przedstawia całkowitą liczbę kwadratów jednostkowych, które mogą się w nim zmieścić i jest mierzona w jednostkach kwadratowych np. cm2, dm2, m2 itd. Romb to równoległobok z przeciwległymi bokami równoległymi, przeciwległymi kątami równymi i sąsiednimi kątami uzupełniającymi. Poniższe właściwości służą do definiowania rombu:
- Romb jest czworobokiem równobocznym. Wszystkie jego boki są równej długości.
- W rombie przekątne przecinają się pod kątem prostym.
- Przekątne to dwusieczne kąta.
- Pole rombu można obliczyć na trzy różne sposoby:
- za pomocą podstawy i wysokości,
- za pomocą przekątnych
- za pomocą trygonometrii.
Jak obliczyć pole rombu?
Do obliczenia powierzchni rombu można użyć różnych wzorów w zależności od znanych nam parametrów. Poniżej znajdziesz trzy metody.
Kiedy podstawa i wysokość są znane
Jak już wiemy, romb to równoległobok. Wiemy też, że powierzchnia równoległoboku jest pomnożona przez mnożenie jednostek podstawy i wysokości kwadratów. Tą samą właściwość możemy zastosować w przypadku rombu, zatem:
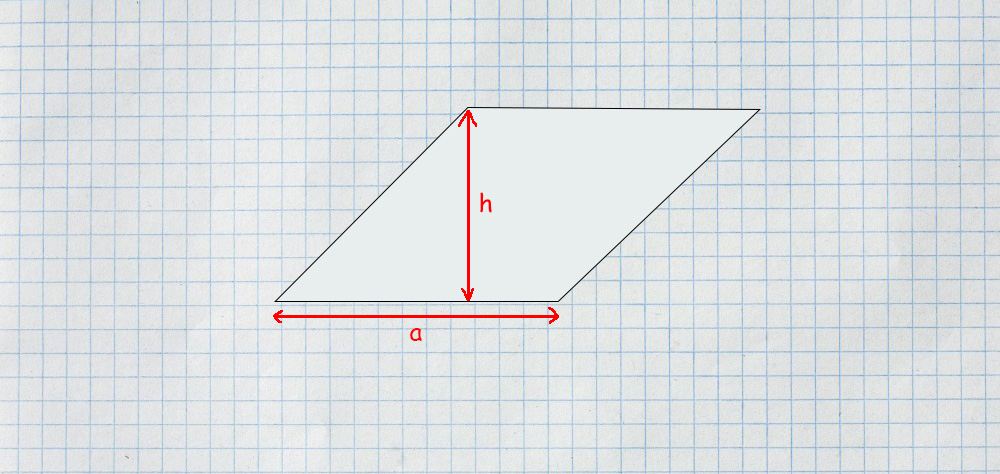
Pole rombu = Podstawa (a) × Wysokość (h)
Jak obliczyć pole rombu za pomocą pomocą podstawy i wysokości?
Krok 1: Znajdź i zanotuj podstawę i wysokość podanego rombu. Podstawa jest jednym z jego boków rombu, a wysokość jest prostopadłą odległością od wybranej podstawy do przeciwnej strony.
Krok 2: Pomnóż podstawę i wysokość. Wynikowa wartość da powierzchnię rombu.
Kiedy znane są przekątne
Korzystając z kolejnej właściwości równoległoboku, można obliczyć pole rombu za pomocą przekątnych. Powierzchnia rombu jest równa połowie iloczynu długości przekątnych. Wzór na obliczenie powierzchni rombu za pomocą przekątnych jest podany wygląda następująco:
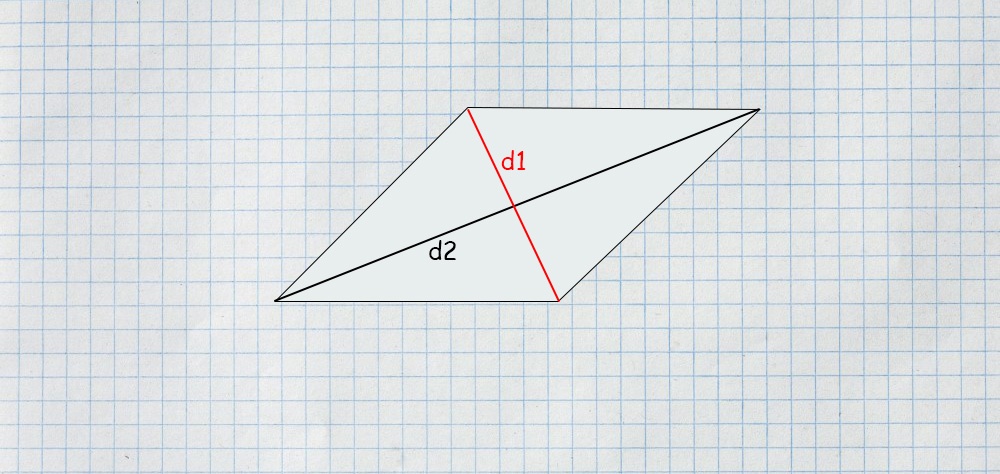
Pole rombu = (przekątna d1 x przekątna d2) / 2
Jak obliczyć pole rombu za pomocą dwóch przekątnych?
Rozważmy romb ABCD, mający dwie przekątne, tj. AC i BD.
- Krok 1: Znajdź długość obu przekątnych, przekątnej 1 i przekątnej 2.
- Krok 2: Pomnóż obie długości, d1 i d2.
- Krok 3: Podziel wynik przez 2. Wynikowa wartość da pole rombów ABCD.
Kiedy znany jest bok i kąty
Ostatnim sposobem na obliczenie pola rombu jest zastosowanie zależności trygonometrycznych w przypadku kiedy znane są boki i kąty. W rzeczywistości możemy wykorzystać dowolny kąt, ponieważ kąty są równe albo są uzupełniające, natomiast te mają ten sam sinus. Wzór na pole powierzchni rombu obliczanej za pomocą boku i kąta wewnętrznego można obliczyć:
Powierzchnia rombu = bok 2 × sin(A)
Powierzchnia rombu = bok 2 × sin(B)
Przykład: Jaka jest powierzchnia rombu, jeśli długość jego boku wynosi 4 metry, a jeden z jego kątów A wynosi 30º.
Rozwiązanie: Pole rombu = s 2 × sin(30º) = 4 2 × 1/2
⇒ Pole rombu = 16 × 1/2 = 8 m2
Porady i wskazówki
- Pamiętaj, że wysokość to nie to samo, co długość boku rombu.
- Pole powierzchni rombu można znaleźć na trzy sposoby: gdy podano przekątne, gdy podano kąt i bok, gdy podano kąt i wysokość.
- Użyj twierdzenia Pitagorasa, aby znaleźć drugą przekątną, jeśli podano miary jednej przekątnej i boku.
Jak obliczyć obwód rombu?
Romb, jak kwadrat, jest specjalnym równoległobokiem, w którym wszystkie ściany boczne są równe. Dzięki temu obliczenie obwodu jest banalnie proste.
Obwód rombu = 4a
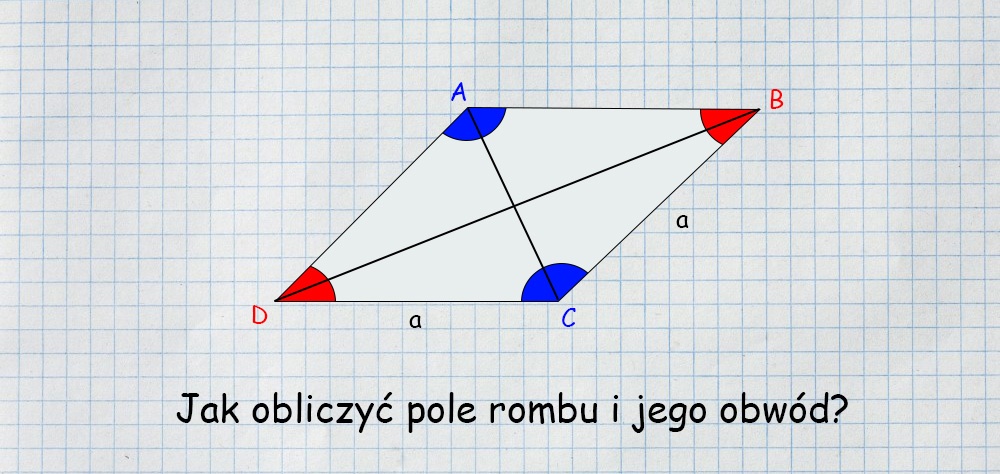
Właściwości kątów i przekątnych w rombie
Jak już wiemy, romb jest złożony z dwóch przekątnych oraz 4 kątów wewnętrznych i możemy przyjąć, że zawsze:
- suma kątów wewnętrznych ma 360 stopni ,
- suma kątów sąsiadujących ma 180 stopni,
- przekątne przecinają się pod kątem prostym,
- przekątne przecinając się tworzą cztery trójkąty prostokątne,
- przecięcie przekątnych tworzy koło wpisane, a więc środek symetrii.